Understanding Area Measurement Formula: A Comprehensive Guide

When it comes to calculating the area of various shapes, understanding the area measurement formula is crucial for students, professionals, and anyone involved in fields requiring spatial analysis. This article delves into the various formulas used to calculate the area of different geometric shapes, providing a detailed examination of their applications and importance. Whether you are a student preparing for a geometry exam or a professional in architecture or engineering, grasping these concepts can enhance your understanding of spatial dimensions and planning.

Area measurement is not just a mathematical concept; it plays a vital role in numerous real-world applications, from land surveying to construction and interior design. By mastering the area measurement formulas, you can effectively solve problems related to space, optimize resource allocation, and enhance your analytical skills.

This guide will explore various area measurement formulas, including those for simple shapes like squares and rectangles, as well as more complex figures like circles and polygons. Additionally, we will provide practical examples and applications to further solidify your understanding of these essential concepts.

Table of Contents

• 1. Introduction to Area Measurement
• 2. Common Area Measurement Formulas
• 3. Area Measurement for Complex Shapes
• 4. Practical Applications of Area Measurement
• 5. Tools for Area Measurement
• 6. Importance of Accurate Area Measurement
• 7. Frequently Asked Questions
• 8. Conclusion

1. Introduction to Area Measurement

The concept of area refers to the measure of the amount of space inside a two-dimensional shape. Understanding the area is fundamental in various fields, including mathematics, engineering, and architecture. The area measurement formula provides a systematic way to calculate the space within different shapes, allowing for precise spatial planning and design.

1.1 What is Area?

Area is defined as the extent of a surface or a two-dimensional shape. It is measured in square units, such as square meters (m²), square feet (ft²), or square inches (in²). The importance of calculating area lies in its application in real-world scenarios, such as determining the size of a plot of land or calculating the amount of paint needed to cover a wall.

1.2 Units of Measurement

Area can be measured in various units, depending on the context. Here are some common units:

• Square meters (m²)
• Square feet (ft²)
• Square yards (yd²)
• Acres
• Hectares

2. Common Area Measurement Formulas

There are several fundamental shapes, each with its own area measurement formula. Below are the most commonly used area formulas for basic geometric shapes:

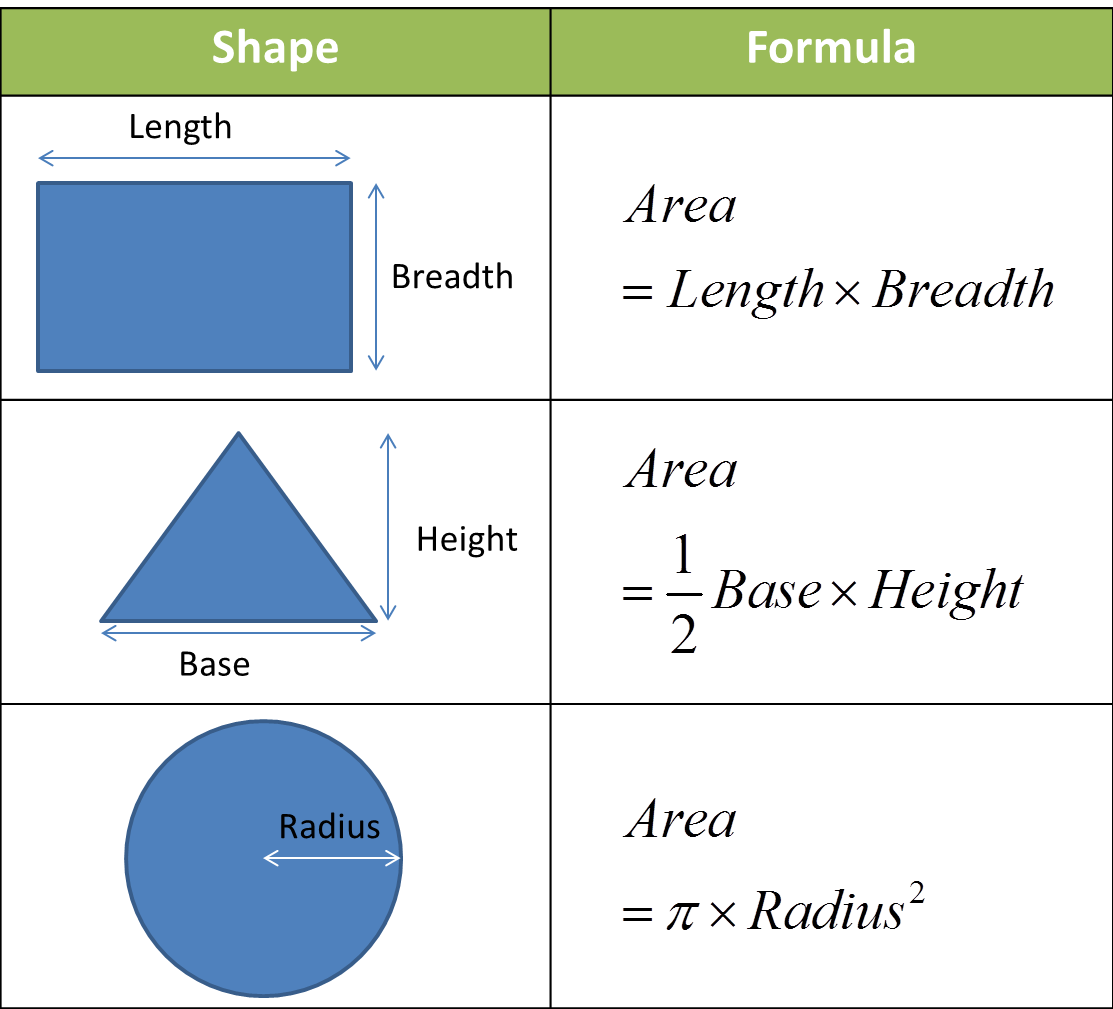
2.1 Area of a Rectangle

The area \( A \) of a rectangle can be calculated using the formula:

A = length × width

2.2 Area of a Square

For a square, where all sides are of equal length, the area is given by:

A = side²

2.3 Area of a Triangle

The area \( A \) of a triangle can be determined using the formula:

A = 1/2 × base × height

2.4 Area of a Circle

To find the area \( A \) of a circle, the formula is:

A = π × radius²

3. Area Measurement for Complex Shapes

In addition to simple shapes, there are formulas for calculating the area of more complex shapes, such as polygons and irregular figures.

3.1 Area of a Parallelogram

The area \( A \) of a parallelogram can be calculated as:

A = base × height

3.2 Area of a Trapezoid

The area \( A \) of a trapezoid can be calculated using the formula:

A = 1/2 × (base1 + base2) × height

3.3 Area of Irregular Shapes

For irregular shapes, one can divide the shape into smaller, regular shapes, calculate their areas, and then sum them up to find the total area.

4. Practical Applications of Area Measurement

Understanding area measurement has various real-world applications, including:

• Land surveying and real estate
• Construction and architecture
• Interior design and landscaping
• Urban planning and development

5. Tools for Area Measurement

Several tools and technologies can assist in measuring area accurately:

• Measuring tape
• Laser distance measurers
• GPS devices
• Mapping software

6. Importance of Accurate Area Measurement

Accurate area measurement is critical in ensuring that projects are completed efficiently and within budget. Inaccurate measurements can lead to costly mistakes, resource wastage, and delays.

7. Frequently Asked Questions

Here are some common questions regarding area measurement:

7.1 How do I calculate the area of an irregular shape?

To calculate the area of an irregular shape, divide it into regular shapes, calculate each area, and then sum them up.

7.2 What units should I use for area measurement?

The unit of measurement depends on the context. For small areas, square meters or feet are commonly used, while larger areas may be measured in acres or hectares.

8. Conclusion

In conclusion, understanding the area measurement formula is essential for various fields and everyday applications. From simple shapes to complex figures, knowing how to calculate area can enhance your analytical skills and contribute to effective planning and execution of projects. We encourage you to practice these formulas and apply them in real-world situations. If you have any questions or comments, feel free to leave them below!

Thank you for reading this comprehensive guide on area measurement formulas. We hope you found it informative and helpful. Be sure to check back for more articles on related topics in mathematics and geometry.